Основы программирования на C++, PASCAL

Begin

If I=1

Then Progres:=AO

Else Progres:=Progres(A0,D,I-1)+D

End;

Следующая программа выводит на экран первые 20 чисел Фибоначчи, значения которых вычисляет рекурсивная функция Fibon.

Var К: Byte;

Function Fibon(N: Integer): Integer;

Begin

If (N=1) Or (N=2)

Then Fibon:=1

Else Fibon:=Fibon(N-1)+Fibon(N-2)

End;

Begin

For K:=l To 20 Do WriteLn(Fibon(K))

End.

Необходимо отметить, что использование рекурсивных функций ведет к замедлению счета. Кроме того, можно столкнуться с проблемой нехватки длины стека, в котором запоминается «маршрут» рекурсивных обращений.

Рекуррентные последовательности часто используются для решения разного рода эволюционных задач, т.е. задач, в которых прослеживается какой-то процесс, развивающийся во времени. Рассмотрим такую задачу.

Пример 6. В ходе лечебного голодания масса пациента за 30 дней снизилась с 96 до 70 кг. Было установлено, что ежедневные потери массы пропорциональны массе тела. Вычислить, чему была равна масса пациента через k дней после начала голодания для k = 1, 2, ..., 29.

Обозначим массу пациента в i-й день через рi (i = 0, 1, 2, ..., 30). Из условия задачи известно, что р0 = 96 кг, p30 = 70 кг.

Пусть К— коэффициент пропорциональности убывания массы за один день.

Тогда

Получаем последовательность, описываемую следующей рекуррентной формулой:

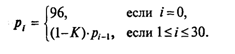
Однако нам неизвестен коэффициент К. Его можно найти, используя условие p30 = 70.

Для этого будем делать обратные подстановки:

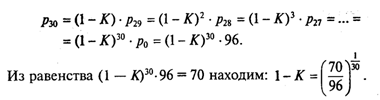
Далее программирование становится тривиальным.

Var I: Byte; P,Q: Real;

Begin

P:=96;

Q:=Exp(l/30*Ln(70/96));

For I:=l To 29 Do

Begin

P:=Q*P;

WriteLn(I,'-й день-',Р:5:3,'кг')

End

End.

Упражнения

1. Рекуррентная последовательность определена следующим образом:

Для данного натурального п получить значение an.

2. Дана последовательность:

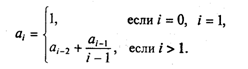
Вычислить произведение элементов с 1-го по 20-й.

3. Используя рекуррентный подход, вычислить сумму многочлена 10-й степени по формуле Горнера, где х — данное вещественное число:

4. Для данного вещественного х и натурального N вычислить цепную дробь: х/(1 + х/(2 + х/(3 + x/(.../(N + х))...).

5. Вычислить и вывести все члены числового ряда

превышающие значение 10-5.

6. Функцию у =

 можно вычислить как предельное значение последовательности, определяемой рекуррентной формулой:

Начальное значение у0 задается произвольно (желательно ближе к

). За приближенное значение корня с точностью ε берется первое уk, для которого выполняется условие: |yk – уk-1| < ε. Составить программу.