Основы программирования на C++, PASCAL

Function Factor(N: Pozint): Pozint;

Begin

If N=0

Then Factor:=1

Else Factor:=N*Factor(N-l)

End;

Предполагается, что тип PozInt объявлен глобально следующим образом:

Type PozInt=0..MaxInt;

Пусть в основной программе для вычисления в целой переменной х значения 3! используется оператор

X:=Factor(3);

При вычислении функции с аргументом 3 произойдет повторное обращение к функции Factor(2). Это обращение потребует вычисления Factor(1). И наконец, при вычислении Factor(0) будет получен числовой результат 1. Затем цепочка вычислений раскрутится в обратном порядке:

Factor(1)=l*Factor(0)=1

Factor(2)=2*Factor(1)=2

Factor(3)=3*Factor(2)=6.

Последовательность рекурсивных обращений к функции должна обязательно выходить на определенное значение. А весь маршрут последовательных вхождений машина запоминает в специальной области памяти, называемой стеком. Таким образом, выполнение рекурсивной функции происходит в два этапа: прямой ход — заполнение стека; обратный ход — цепочка вычислений по обратному маршруту, сохраненному в стеке.

Использование рекурсивных функций — красивый прием с точки зрения программистской эстетики. Однако этот путь не всегда самый рациональный. Рассмотренную задачу с п! можно решить так:

F:=l;

For I:=l To N Do

F:=F*I;

Очевидно, что такой вариант программы будет работать быстрее, чем рекурсивный. И в том случае, когда важнейшим является сокращение времени выполнения программы, следует отдать предпочтение последнему варианту.

В каждой конкретной реализации Паскаля имеется ограничение на количество рекурсивных обращений к подпрограмме (глубина рекурсии). Это связано с ограничением на размер стека. По этой причине можно попасть в ситуацию, когда рекурсивной подпрограммой вообще не удастся воспользоваться.

Рекурсивно определена может быть не только функция, но и процедура. Примеры использования рекурсивно-определенных процедур рассматриваются в пятой главе.

Упражнения

1. Составить программу вычисления площади кольца по значениям внутреннего и внешнего радиусов, используя подпрограмму вычисления площади круга (2 варианта: с процедурой и с функцией).

2. По координатам вершин треугольника вычислить его периметр, используя подпрограмму вычисления длины отрезка, соединяющего две точки.

3. Даны три целых числа. Определить, сумма цифр которого из них больше. Подсчет суммы цифр организовать через подпрограмму.

4. Определить площадь выпуклого четырехугольника по заданным координатам вершин. Использовать подпрограмму-функцию вычисления длины отрезка и подпрограмму-процедуру вычисления площади треугольника по формуле Герона.

5. Описать рекурсивную функцию pow(x, n) от вещественного х (х ≠ 0) и целого п, которая вычисляет величину хn по формуле

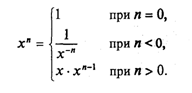
6. Даны натуральные числа п и т; найти НОД (n, т). Использовать программу, включающую в себя рекурсивную процедуру вычисления НОД, и основанную на соотношении НОД (n, т) = НОД (т, r), где r — остаток от деления п на т.