Основы программирования на C++, PASCAL

6.8. Задачи по теме «Двумерные массивы»

6.8.1. Задачи на формирование массивов

В задачах 1—12 сформировать квадратную матрицу порядка n по заданному образцу:

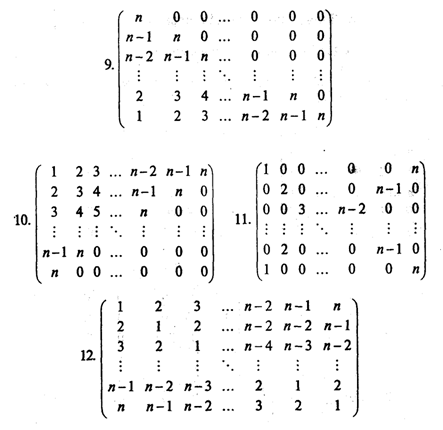
13. Построить квадратную матрицу порядка 2n:

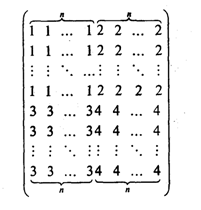
14. Дано действительное число х. Получить квадратную матрицу порядка n +1:

15. Даны действительные числа а1, а2,..., аn. Получить квадратную матрицу порядка n:

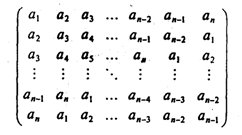
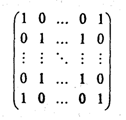
16. Получить матрицу:

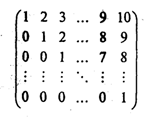
17. Получить матрицу:

18. Составить программу, которая заполняет квадратную матрицу порядка n натуральными числами 1, 2, 3, ..., n2, записывая их в нее «по спирали».

Например, для п = 5 получаем следующую матрицу:

19. Дана действительная квадратная матрица порядка 2n. Получить новую матрицу, переставляя ее блоки размера п х п по часовой стрелке, начиная с блока в левом верхнем углу.

20. Дана действительная квадратная матрица порядка 2n. Получить новую матрицу, переставляя ее блоки размера п х п крест-накрест.

21. Дан линейный массив x1, x2,..., xn-1, xn. Получить действительную квадратную матрицу порядка п:

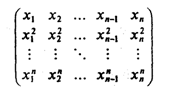
22. Дан линейный массив x1, x2,..., xn-1, xn. Получить действительную квадратную матрицу порядка п:

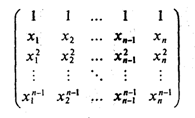
23. Получить квадратную матрицу порядка п:

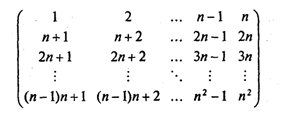
24. Получить квадратную матрицу порядка п:

25. Магическим квадратом порядка п называется квадратная матрица размера п х п, составленная из чисел 1, 2, ..., n2 так, что суммы по каждому столбцу, каждой строке и каждой из двух больших диагоналей равны между собой. Построить такой квадрат.

Пример магического квадрата порядка 3:

6.8.2. Операции с элементами массивов

1. Вычислить сумму и число положительных элементов матрицы A[N, N], находящихся над главной диагональю.

2. Дана матрица А размером п х т. Определить k — количество особых элементов массива А, считая его элемент особым, если он больше суммы остальных элементов его столбца.

3. Задана квадратная матрица. Поменять местами строку с максимальным элементом на главной диагонали со строкой с заданным номером т.

4. Дана матрица B[N, M]. Найти в каждой строке матрицы максимальный и минимальный элементы и поменять их местами с первым и последним элементом строки соответственно.

5. Дана целая квадратная матрица п-го порядка. Определить, является ли она магическим квадратом, т.е. такой, в которой суммы элементов во всех строках и столбцах одинаковы.

6. Элемент матрицы