Основы программирования на C++, PASCAL

3.14. Вычисление рекуррентных последовательностей

Рекуррентная последовательность. Из курса математики известно понятие рекуррентной последовательности. Это понятие вводится так: пусть известно k чисел a1, ..., аk. Эти числа являются первыми числами числовой последовательности. Следующие элементы данной последовательности вычисляются так:

Здесь F— функция от k аргументов. Формула вида

называется рекуррентной формулой. Величина k называется глубиной рекурсии.

Другими словами, можно сказать, что рекуррентная последовательность — это бесконечный ряд чисел, каждое из которых, за исключением k начальных, выражается через предыдущие.

Примерами рекуррентных последовательностей являются арифметическая (1) и геометрическая (2) прогрессии:

Рекуррентная формула для указанной арифметической прогрессии:

Рекуррентная формула для данной геометрической прогрессии:

Глубина рекурсии в обоих случаях равна единице (такую зависимость еще называют одношаговой рекурсией). В целом рекуррентная последовательность описывается совокупностью начальных значений и рекуррентной формулы. Все это можно объединить в одну ветвящуюся формулу. Для арифметической прогрессии:

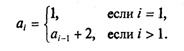
Для геометрической прогрессии:

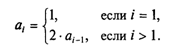
Следующая числовая последовательность известна в математике под названием чисел Фибоначчи:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

Начиная с третьего элемента каждое число равно сумме значений двух предыдущих, т. е. это рекуррентная последовательность с глубиной равной 2 (двухшаговая рекурсия). Опишем ее в ветвящейся форме:

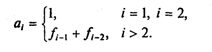
Введение представления о рекуррентных последовательностях позволяет по-новому взглянуть на некоторые уже известные нам задачи. Например, факториал целого числа п! можно рассматривать как значение n-го элемента следующего ряда чисел:

Рекуррентное описание такой последовательности выглядит следующим образом:

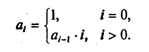
Программирование вычислений рекуррентных последовательностей. С рекуррентными последовательностями связаны задачи такого рода:

1) вычислить заданный (n-й) элемент последовательности;

2) математически обработать определенную часть последовательности (например, вычислить сумму или произведение первых n членов);

3) подсчитать количество элементов на заданном отрезке последовательности, удовлетворяющих определенным свойствам;