Основы программирования на C++, PASCAL

Из подпрограммы В22 можнообратиться только к B21, B1, А. Объясните сами почему.

Все понятно? Если нет, то прочитайте еще раз этот раздел. Очень важно в нем разобраться.

Если одно и то же имя описано во внешнем блоке (глобально) и во внутреннем блоке (локально), то последнее описание (локальное) перекрывает первое в пределах внутреннего блока. Рассмотрим следующий пример:

Program Example1;               Program Example2;

Var X: Integer;                 Var X: Integer;

Procedure P;                    Procedure P;

Var X: Integer;                 Begin

Begin WriteLn('x=',X)               WriteLn('x=',X)

End;                            End;

Begin X:=1;                     Begin X:=l;

P                                     P

End.                            End.

Что выведется на экран в результате работы программы Example1 и Example2? Первая программа выдаст результат:

х=...

На месте многоточия будет какое-то произвольное значение, соответствующее неопределенной величине х. Вторая программа в результате даст

х=1

В первом случае переменная с именем х описана как глобально, так и локально. Но процедура выводит значение локальной переменной, которой ничего не присвоено. В этом примере идентификатором х обозначены две совершенно разные величины, им соответствуют две разные ячейки памяти.

Во втором примере переменная х одна на всю программу. Она описана глобально. Поэтому значение 1, присвоенное ей в основной программе, передается и в подпрограмму.

Далее разговор пойдет о ситуации на первый взгляд совершенно парадоксальной. Оказывается, подпрограмма в своем описании может содержать обращение к самой себе. Такая подпрограмма называется рекурсивной.

Рекурсивные подпрограммы. В математике рекурсивным называется определение любого понятия через самое себя. Классическим примером является определение факториала целого числа, большего или равного нулю:

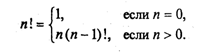
Здесь функция факториала определена через факториал. Нетрудно понять справедливость такого определения. Для п > 0

Вариант 0!=1 является тривиальным. Но это «опорное» значение, от которого начинается раскручивание всех последующих значений факториала:

Рассмотрим подпрограмму-функцию, использующую в своем описании приведенную выше рекурсивную формулу.