Основы программирования на C++, PASCAL

то обобщенная формула для i-го элемента будет следующей:

Нетрудно увидеть, что между элементами данной последовательности имеется рекуррентная зависимость. Ее можно найти интуитивно, но можно и вывести формально. Правда, для этого нужно догадаться, что рекурсия — одношаговая, и что каждый следующий элемент получается путем умножения предыдущего на некоторый множитель, т.е.

Используя обобщенную формулу, имеем:

Отсюда:

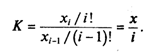
Действительно:

Следовательно, данная рекуррентная последовательность может быть описана следующим образом:

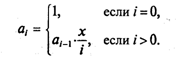
И наконец, приведем программу, решающую поставленную задачу.

Var A,X,S,Eps: Real;

I: Integer;

Begin

Write('X ='); ReadLn(X);

Write('Epsilon ='); ReadLn(Eps);

A:=l; S:=0; I:=0;

While Abs(A)>Eps Do

Begin

S:=S+A;

I:=I+1;

A:=A*X/I

End;

WriteLn('Сумма ряда равна', S:10:4)

End.

Как и прежде, значения одношаговой рекуррентной последовательности вычисляются в одной переменной.

Каждое повторное выполнение цикла в этой программе приближает значение S к искомому (уточняет значащие цифры в его записи). Такой вычислительный процесс в математике называется итерационным процессом. Соответственно, циклы, реализующие итерационный вычислительный процесс, называются итерационными циклами. Для их организации используются операторы While или Repeat.

Пример 5. Для заданного натурального N и вещественного х (х > 0) вычислить значение выражения:

В этом случае рекуррентность не столь очевидна. Попробуем найти ее методом индукции. Будем считать, что искомое выражение есть N-й элемент последовательности следующего вида:

Отсюда видна связь:

Теперь поставленная задача решается очень просто:

Var A,X: Real; I,N: Integer;

Begin

Write('X='); ReadLn(X);

Write('N='); ReadLn(N);

A:= Sqrt(X);

For I:=2 To N Do

A:=Sqrt(X+A);

WriteLn('Ответ:',А)

End.

К решению всех перечисленных выше задач можно подойти иначе.

Вспомним о рекурсивно определенных подпрограммах. Посмотрите на описание арифметической прогрессии в форме рекуррентной последовательности. Из него непосредственно вытекает способ определения функции для вычисления заданного элемента прогрессии.

Сделаем это для общего случая, определив арифметическую прогрессию с первым членом а0 и разностью d:

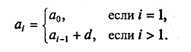
Соответствующая подпрограмма-функция выглядит так:

Function Progres(АО,D: Real;I: Integer): Real;